Больше кубитов — меньше ошибок? Да, но торопиться не надо…
Около трёх десятилетий над квантовыми вычислителями — которые активно прорабатывались тогда в теории и начинали потихоньку воплощаться и в металле (без кавычек: на одни только охлаждающие системы для сверхпроводящих кубитов уходят центнеры высокочистой меди) — дамокловым мечом висела проблема нарастающей сложности коррекции квантовых ошибок. Имеется в виду, что квантовые вычисления и так довольно неточны (в лучшем случае речь идёт об 1 ошибке на 10 тыс. операций, т. е. о частоте встречаемости сбоев 10−4, а чаще и вовсе 10−3, — катастрофическое отставание от характерного для полупроводниковых фон-неймановских систем показателя, 10−10 и менее), а с ростом числа узлов — кубитов — в системе, как напрямую следует из теории вероятности, ошибки должны проявляться только чаще. И вот 105-кубитный квантовый процессор Willow, представленный Google в начале декабря, впервые в истории преодолел это принципиальное, казалось, ограничение — и при решении тестовой задачи допустил примерно в два раза меньше ошибок за цикл вычислений, чем построенный по той же архитектуре 72-кубитный.
Казалось бы, вот он, принципиальный прорыв на квантовом фронте, ведь теперь чем больше в одном чипе кубитов, тем меньше квантовые вычислители станут допускать ошибок! А потому, в частности, плакала вся неквантовая криптография, а заодно и построенные на позаимствованных у неё алгоритмах ECDSA и SHA-256 криптовалюты и умные контракты. Раз генерируемые по этим алгоритмам шифры теперь принципиально взламываемы, то при выходе числа логических кубитов в квантовой системе на уровень около 2,5 тыс. (у Willow, напомним, пока что 105 физических) всё, что закодировано по доквантовым стандартам, перестанет быть тайной! Вот и сама Google уже планирует к концу текущего десятилетия создать полноценный отказоустойчивый квантовый компьютер (надо полагать, со множеством логических кубитов, иначе зачем огород городить?), чтобы предоставлять заказчикам доступ к нему через облако! То есть в лучшем случае всего-то лет пять остаётся на суматошный всеинтернетный срочнопереход к квантовоустойчивым методам шифрования. Который даже страшно представить, в какие суммы обойдётся, если учесть, насколько распространены сегодня криптотранзакции, начиная от самых простейших, вроде обращения к веб-сайтам по защищённому протоколу HTTPS!
Но если вдуматься — так ли уж серьёзна нависшая над доквантовой криптографией опасность? И вообще, за счёт чего — а главное, в каких пределах — архитектуре Willow удалось преодолеть барьер нарастания сложности с числом кубитов?

Внешне серийный корпусированный квантовый процессор не так уж просто отличить от фон-неймановского, тем более что технологии их изготовления схожи (источник: Google)
⇡#Квантовый объект своими руками
Человечество давным-давно освоило искусство создавать высоконадёжные системы из компонентов, скажем так, склонных к отказу: проблемные узлы следует дублировать, страивать, даже учетверять — словом, создавать «горячий резерв», готовый приниматься за работу в случае выхода из строя основного агрегата. В одной из давних статей о квантовых вычислениях мы упоминали уже, что коррекция ошибок через привлечение к контролю над операциями одного кубита других, квантово с ним запутанных, — чрезвычайно распространённый в этой отрасли метод. Но у него, увы, имеется принципиальное ограничение: если слишком уж увлечься исправлением ошибок на одном из участков квантовой системы, можно в погоне за гарантированно высокой надёжностью настолько эту систему переусложнить, что время появления очередной ошибки окажется меньше, чем интервал, на котором многокубитная система сохраняет своё самое главное квантовое свойство: взаимную запутанность всех своих компонентов. И вот как раз с протяжённостью этого интервала — с временем сохранения когерентности, coherence time, — у зарядовых кубитов (charge qubits), что изготавливаются классическими методами производства полупроводников, немало проблем. Но именно на такого рода кубитах и построен квантовый процессор Google Willow («Ива» — один из возможных вариантов перевода).
Вообще говоря, время сохранения когерентности напрямую зависит от физической реализации той квантовой системы, что ложится в основу данного конкретного квантового вычислителя. Если за базовые «кирпичики» квантового компьютера брать естественные квантовые объекты — например, единичные ионы, — то для них время сохранения когерентности может исчисляться десятками минут. Однако построение даже одноионных, не говоря уже о многокубитных, квантовых компьютеров сталкивается со множеством иных принципиальных трудностей, на фоне которых продолжительное удержание когерентного состояния — выигрыш, бесспорно, но не так уж прямо чтобы решающий.
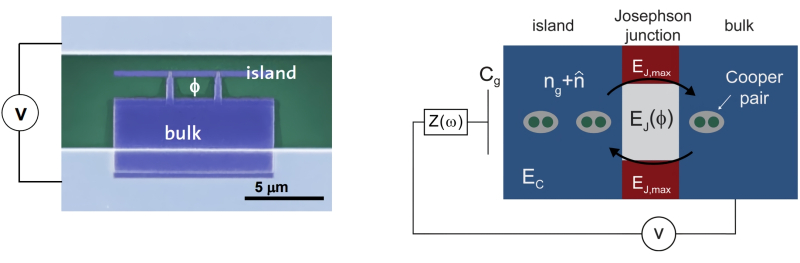
Слева: поперечное сечение зарядового кубита; показаны массивный сверхпроводник — резервуар куперовских пар (bulk) и загончик, он же островок (island); длина масштабного отрезка — 5 мкм. Справа — электрическая схема работы джозефсоновского перехода; сравнительные размеры резервуара, загончика и куперовских пар не согласованны (источник: ETH)
Другой путь — создавать «искусственные атомы»; некие заведомо макроскопические системы, готовые при определённых условиях демонстрировать квантовые свойства. Одно из наиболее перспективных направлений здесь — сверхпроводящие миниатюрные контуры, реализующие эффект Джозефсона. Но вот для них характерные времена сохранения когерентности составляют в лучшем случае десятые доли миллисекунд, что, ясное дело, неимоверно затрудняет любые усилия — во-первых, по своевременному выявлению ошибок при квантовых вычислениях, а во-вторых — по их исправлению до того момента, как когерентность данной квантовой системы прекратится по естественным причинам: из-за влияния теплового шума от соседних (неквантовых) компонентов вычислителя, к примеру.
Впрочем, даже с учётом этого такая разновидность искусственных атомов, как зарядовые кубиты, крайне привлекательна в практическом плане. Их компоненты без особых затруднений изготавливают методами полупроводниковой электронно-лучевой литографии, причём с применением вполне зрелых по сегодняшним меркам техпроцессов — даже не «нанометрового» класса. Иными словами, зарядовые кубиты, в том числе их наиболее популярную сегодня реализацию, трансмоны (transmon), лежащие и в основе Willow тоже, — можно серийно выпускать на микропроцессорных фабриках не самого последнего поколения. И с этой точки зрения с зарядовыми кубитами куда проще экспериментировать, подыскивая различные пути для наращивания времени сохранения когерентности и/или для сокращения частоты ошибок в ходе вычислений с использованием базирующихся на них систем. Чем, собственно, квантовая команда Google (и не только она одна) усердно занималась последние годы.
По сути, Willow относится к разряду сверхпроводящих квантовых интегральных схем: его кубиты оперируют не степенями свободы некоего природного квантового объекта (фотона, электрона, иона), а коллективными электродинамическими модами макроскопических электронных компонентов, из которых такой кубит составлен. Базовая конструкция контура с джозефсоновским переходом — это два сверхпроводника, разделённые действительно тонким (одно-двухнанометровым) слоем либо диэлектрика, либо несверхпроводящего вещества. Через этот разрыв обычные электроны проводимости проникать не могут, зато куперовские пары — ведущие себя как единая частица квантовые объекты, состоящие из связанных электронов с противоположно направленными спинами, за счёт которых как раз и реализуется эффект сверхпроводимости, — вполне, причём без какого бы то ни было сопротивления. И это очень кстати: ведь квантовые интегральные схемы в любом случае не вышло бы реализовать с применением обычных для микроэлектроники транзисторов. Чтобы макроскопическая система проявляла квантовые свойства, она обязана быть недиссипативной, т. е. не рассеивать в пространство (не переводить в тепло) энергию в процессе изменения своего состояния. Как раз сверхпроводники при температуре ниже критической и обладают нулевым сопротивлением — при прохождении через них тока тепло не рассеивают. Транзисторы же, увы, недиссипативными не бывают.

Экспериментальная двухкубитная система, построенная для изучения взаимодействия зарядовых кубитов; сами кубиты — квадратные конструкции с вертикальными линиями (представляющими, собственно, джозефсоновские переходы) слева внизу и справа вверху (источник: IBM)
Но каким же образом джозефсоновский туннельный переход заменяет негодный (в смысле, диссипативный, а потому неподходящий для построения квантовой макросистемы) транзистор, если проявляется пресловутый эффект — именно за который британский физик Брайан Джозефсон (Brian David Josephson) получил в 1973 г. половину Нобелевской премии — всего лишь в трансгрессии электронных пар сквозь непреодолимую для неквантовых объектов преграду? Иными словами, как проводящий участок контура, тот самый квантовый туннель, позволяет реализовать характерную для транзистора нелинейность — благодаря которой, собственно, и возможно проводить на полупроводниковых контурах логические операции, меняя движение зарядов и накапливая их?
Обычный, неквантовый проводник (с сопротивлением; всем знакомый резистор) — линейный, т. е. зависимость тока от напряжения для него постоянна. Зарядовый же кубит оказывается нелинейным благодаря особой конструкции: два «берега» джозефсоновского перехода в данном случае существенно различаются по конструкции. Один из сверхпроводников в составе зарядового кубита — сравнительно массивный; он служит резервуаром куперовских пар. Второй, отделённый от первого нанометровой преградой, и сам по себе тоже наноразмерен; его нередко прямо называют «вмещающим всего одну куперовскую пару загончиком» (single Cooper-pair box; в русскоязычной литературе часто используется термин «островок»). Строго говоря, куперовских пар в этом загончике может быть и две, и три, и более, — главное, что целое число; т. е. полученная макроскопическая система квантуется. Дальше — дело техники (точнее, математики): решение стационарного уравнения Шрёдингера для описанной системы с джозефсоновским переходом показывает, что зарядовый кубит может обладать лишь одним из двух разрешённых значений энергии, причём в первом из них состоянии загончик-островок как физический объект электрически нейтрален, а во втором — его заряд равен сумме зарядов перебравшихся на него за счёт туннельного эффекта избыточных куперовских пар (в базовом случае такая пара всего одна).
⇡#Раз кубит, два кубит, посредине тоже
Собственно, вот она, квантовая макроскопическая система: два предельных состояния, описываемые уравнением Шрёдингера, и квантовая неопределённость до момента измерения — поскольку куперовские пары могут свободно и без сопротивления (сверхпроводимость же!) перемещаться через туннель как угодно даже в отсутствие внешнего — управляющего — напряжения. Технически зарядовый кубит реализуется подведением к наноразмерному загончику двух электродов (обычно это выполненные литографическим способом металлические дорожки шириной в несколько десятков нанометров): один используют для управления состоянием кубита, второй — для контроля этого состояния. Подача на управляющий электрод короткого, около 50 пикосекунд, импульса определённой величины и полярности приводит к перемещению строго одной куперовской пары в загончик; обратного по знаку — к возвращению этой пары в резервуар, представленный большим электродом.
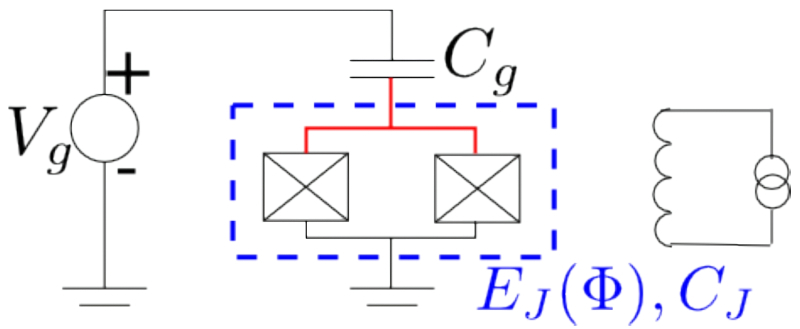
Трансмон — разновидность зарядового кубита, в которой задвоенные джозефсоновские переходы (перечёркнутые квадраты на электрической схеме a) дополнительно шунтированы конденсатором большой ёмкости ради пущей стабильности системы, что позволяет довести длительность сохранения когерентности до сотен микросекунд (источник: Yale University)
А дальше — самое интересное: более продолжительный (но не более мощный!) управляющий импульс переводит волновую функцию зарядового кубита в гибридное состояние, при котором по-прежнему единственная куперовская пара находится в загончике лишь частично: напомним, что длина когерентности куперовских пар — типичное расстояние, на котором образующие такую пару электроны эффективно взаимодействуют (за счёт обмена фононами), — составляет около 100 нм, что заведомо превосходит ширину зазора между резервуаром и загончиком. Такая реализация принципа квантовой суперпозиции позволяет, регулируя длительность короткого импульса напряжения на управляющем электроде, выполнять над кубитом различные квантовые логические операции. По сути, зарядовый кубит — в полном смысле слова «искусственный атом», где разрешённые состояния двух первых электронных орбиталей моделируются нижним и верхним состояниями системы (нейтральный загончик — загончик с единственной куперовской парой). Впервые на практике действующий зарядовый кубит был продемонстрирован исследователями из японской NEC ещё в 1999 г.
Единичный зарядовый кубит с характерными размерами от единиц до сотен микрометров, подчеркнём ещё раз, — макроскопический объект. А это значит, что он с неизбежностью неидеален: если все природные квантовые объекты совершенны (в том смысле, что невозможно бытие дефектного электрона, например: он или существует во всей полноте присущих ему свойств, тем более что самих-то этих свойств не так уж много — лептонное число, спин, масса да заряд, — или распадается на другие частицы), то микроскопический контур с джозефсоновским переходом — нет. Как раз из-за наличия неизбежных дефектов в конструкции искусственных атомов — будь то неоднородная толщина слоя диэлектрика в джозефсоновской щели, или небольшой сбой в продолжительности/интенсивности/профиле управляющего импульса, или ещё что-нибудь — продолжительность пребывания такой квантовой системы в когерентном состоянии изрядно, по сравнению с природными квантовыми системами, ограничена. Декогеренция же зарядовых кубитов приводит к утрате суперпозиции и к выходу их из квантового состояния (хотя сверхпроводимость при этом никуда не девается, если температурный режим в норме), причём под действием не только внутренних дефектов, но и крайне трудно отсекаемых внешних воздействий — флуктуаций всё той же температуры, вибраций, магнитных полей, электромагнитного излучения и проч. А если кубит в квантовом вычислителе не один и их приходится взаимно запутывать (entangle), чтобы производить многокубитные вычисления, сложность решения инженерной задачи по продлению времени когерентности возрастает экспоненциально — с числом задействованных кубитов.
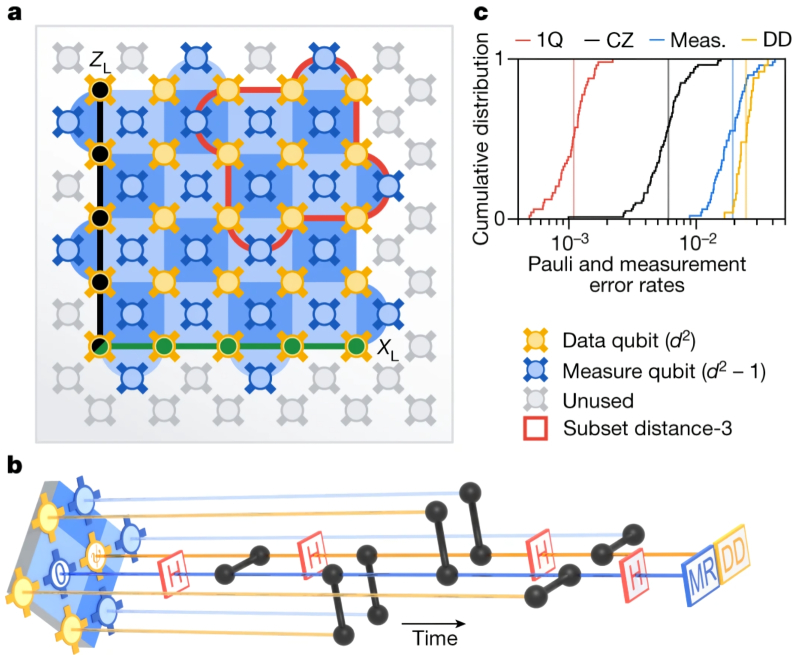
Общий принцип исправления квантовых ошибок в 72-кубитном процессоре Sycamore (созданном на тех же физических принципах, что и Willow): a) схема применения алгоритма поверхностного кода d-5 для 25 рабочих кубитов в матрице 5×5 (жёлтые кружки) и 24 контрольных; b) замеры накопительного распределения ошибок, свидетельствующие о повышении точности с ростом числа физических кубитов в составе одного логического; c) наглядная демонстрация того, какие именно ошибки потери попарной когерентности исправляет поверхностный код (источник: Google)
И здесь мы снова возвращаемся к поднимавшемуся уже вопросу об алгоритмической коррекции ошибок. Не повторяя в деталях прежний наш рассказ о принципах её организации, напомним лишь, что от физических кубитов для решения предметных задач исследователи переходят к логическим, где каждый логический — в зависимости от выбранного алгоритма коррекции — может быть образован и тремя, и пятью, и девятью, и семнадцатью физическими, — и даже это далеко ещё не предел. Проблема здесь в том, что просто пустить квантовые вычисления по трём, скажем, параллельным потокам и на каждом этапе сравнивать состояния трёх исполняющих их кубитов не выйдет: произведённое измерение выводит систему из квантового состояния в классическое, и вычисления прерываются. Поэтому контрольные кубиты запутываются с рабочими, затем сопоставляются измеренные показания контрольных в определённом порядке, после чего контрольные снова запутываются с рабочими и т. д. Задачу крайне усложняет разнородность ошибок, неизбежно возникающих в ходе квантовых вычислений: каждый их тип приходится выявлять и корректировать по отдельности.
Один из наиболее эффективных алгоритмов квантовой коррекции ошибок, как раз прекрасно подходящий для располагающихся ровными рядами на плоскости зарядовых кубитов, предложил ещё в 1990-х годах российский физик Алексей Китаев. Часто о нём говорят просто как о «поверхностном коде» (surface code), но на практике нередко реализуется вариант «торического кода» (toric code): если взять немнущийся лист бумаги в клеточку и согнуть его в трубку так, чтобы верхний ряд клеточек соприкоснулся с нижним, а затем согнуть ещё раз, но теперь уже стыкуя один с другим торцы полученной трубки, то выйдет как раз тор (бублик) — топологический эквивалент исходного участка плоскости с замыканиями верхней—нижней и левой—правой границ (более корректно это именуется «периодическими граничными условиями»). Поскольку такой подход позволяет задействовать контрольные кубиты наиболее полно (т. е. для рабочих кубитов, находящихся на границе, не нужно дополнительно выстраивать корректирующие схемы вовне, — достаточно электрически соединить их с теми уже имеющимися контрольными, что расположены на другом, противоположном краю), в прикладном плане это едва ли не идеальный вариант.
Итак, на плоскости квантового процессора на зарядовых кубитах эти самые кубиты располагаются в шахматном порядке: «белые клетки» — рабочие, «чёрные» — контрольные. Таким образом, каждый рабочий кубит контактирует с четырьмя контрольными, а каждый контрольный — с четырьмя рабочими. Мы не будем останавливаться на детальном описании поверхностного кода в приложении к зарядовым кубитам, скажем лишь, что ещё в 2018 г. квантовая лаборатория Google именно с его помощью успешно реализовала 72-кубитную версию квантового процессора (прямого предшественника нынешнего 105-кубитного, носившего название Bristlecone) — и удостоверилась, что выявлению и исправлению «на лету» подаются ошибки не только первого, но и второго уровня. Собственно, самая первая версия предшественника Willow из 17 физических кубитов содержала, помимо 9 рабочих, ещё и 6 контрольных кубитов. И если один из этих контрольных менял своё состояние, тогда как все прочие его сохраняли, становилось понятно, что соседний (и запутанный) с ним рабочий кубит оказался подвержен ошибке. Какой именно рабочий и какой именно ошибке (bit-flip либо phase-flip), как раз и показывало точное расположение «засбоившего» контрольного кубита. Чтобы понять, как именно достигается здесь стопроцентная определённость, интересующимся придётся чуть глубже погрузиться в принцип действия поверхностного алгоритма.
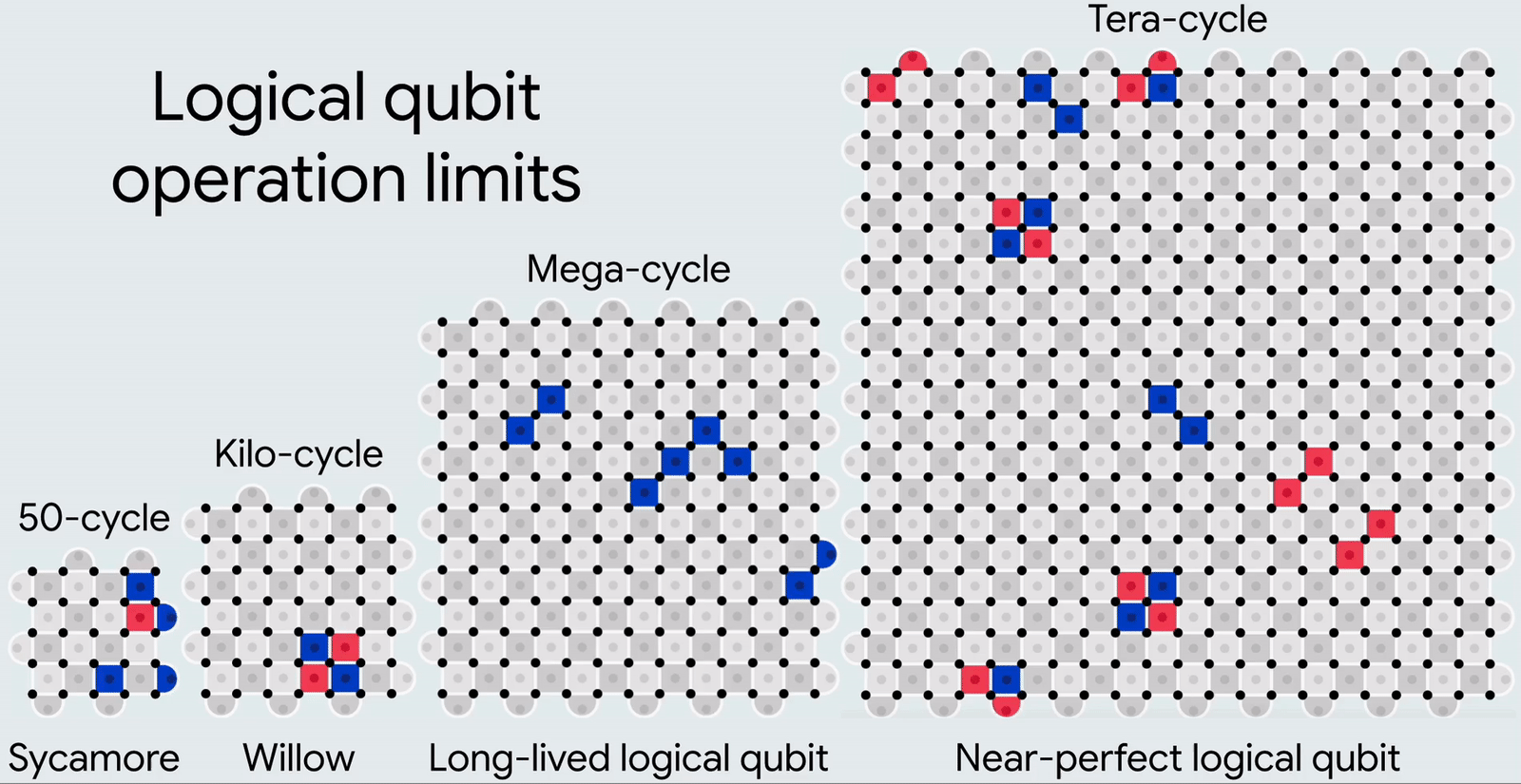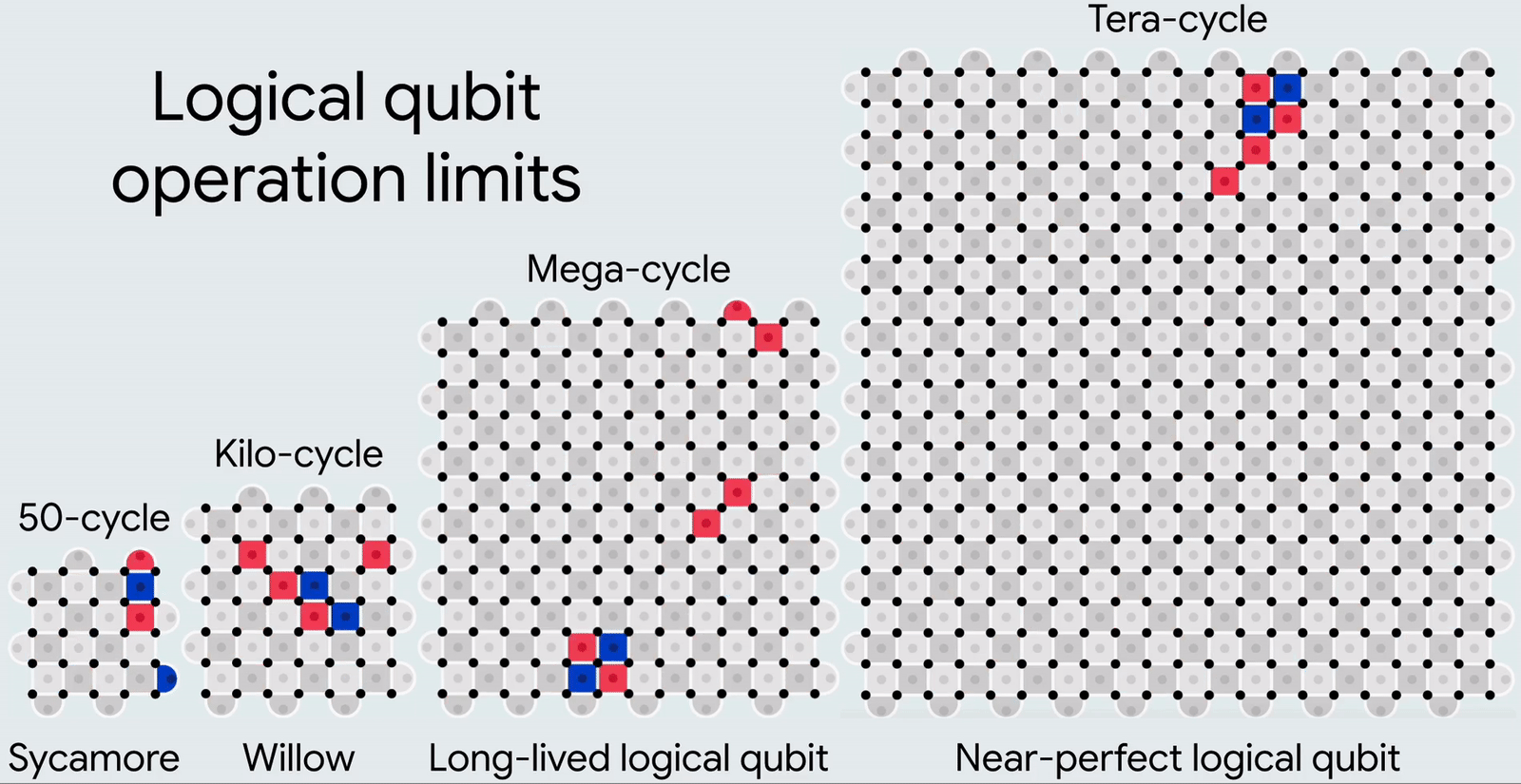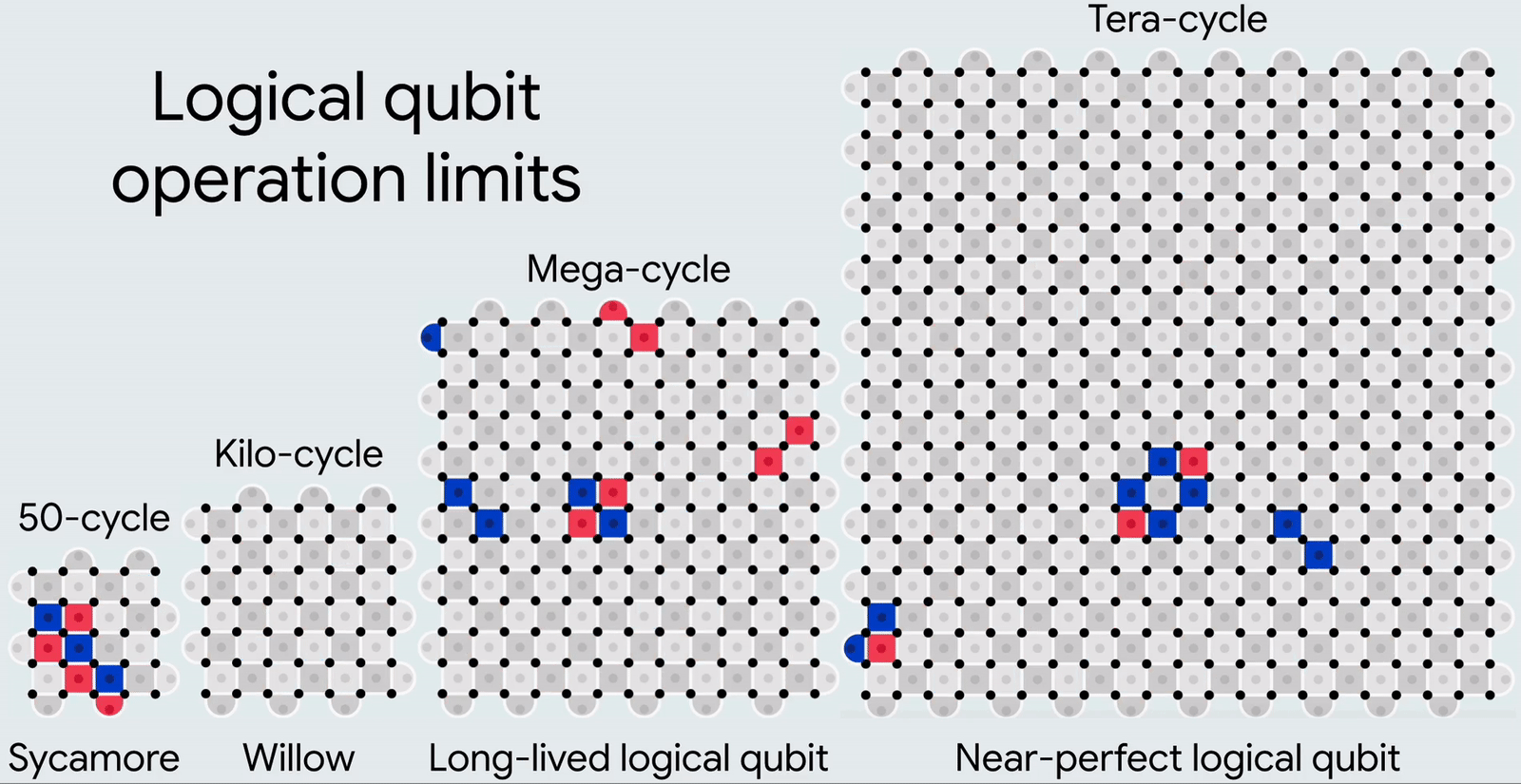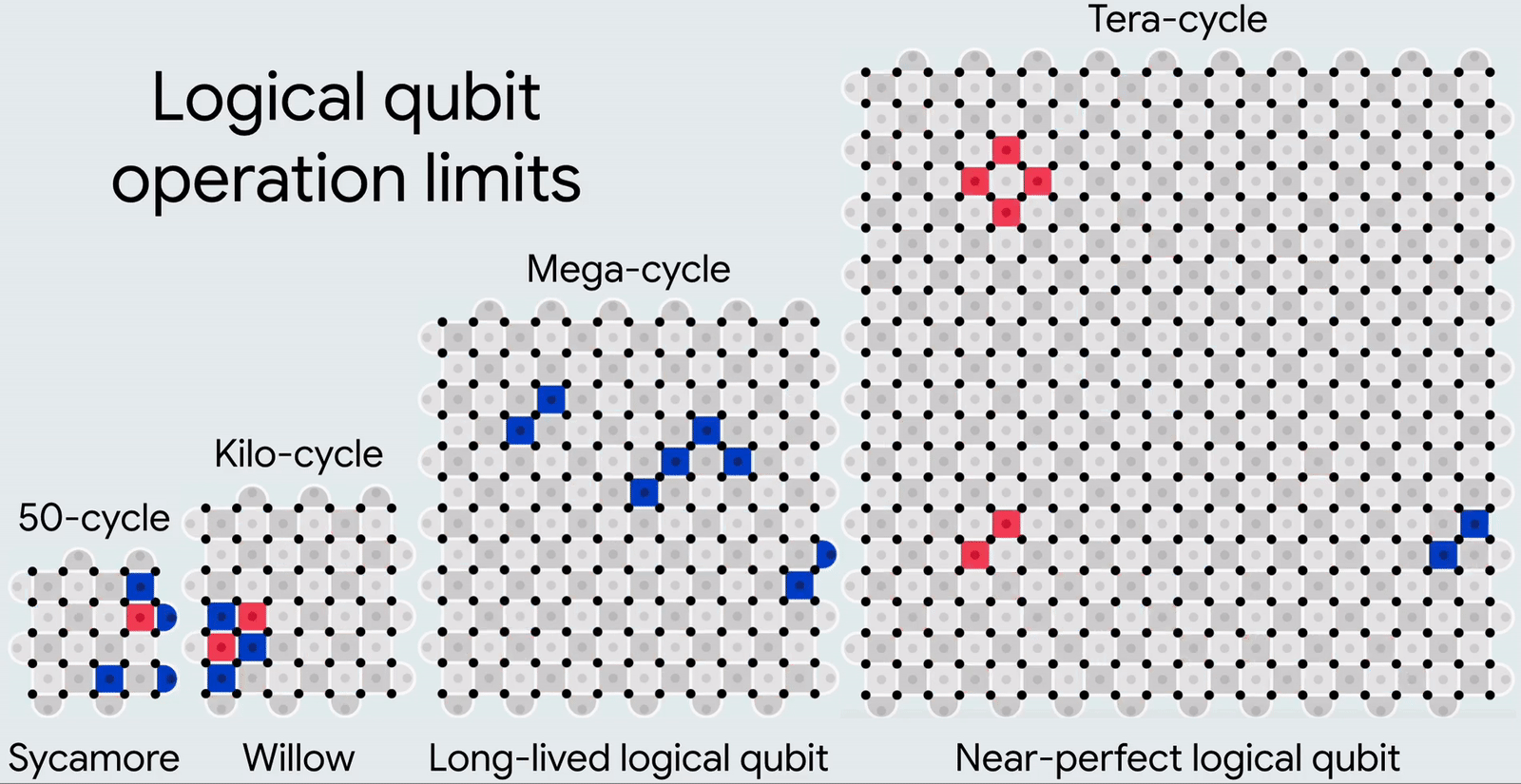
Динамичная иллюстрация того, как с ростом числа физических кубитов росла (от Sycamore к Willow) и будет расти далее (в перспективных архитектурах) точность вычислений и, соответственно, число последовательных циклов этих самых вычислений, производимых без ошибок. Слева направо это число составляет: 50, 1 тысячу, 1 миллион и 1 триллион (1012) циклов (источник: Google)
Главное же для нас в данном случае то, что для конструкции с 9 рабочими кубитами, расположенными матрицей 3×3, требуется 6 контрольных, — это и есть 17-кубитный, самый первый предшественник Willow, относящийся к 2016 г. Соответствующий алгоритм коррекции называется distance-3 surface code, или попросту d-3 (тройка здесь указывает на размерность квадратной матрицы рабочих кубитов), и благодаря ему система точно определяет, а затем и корректирует любую одиночную ошибку. Проблема в том, что даже на протяжении недолгого времени сохранения когерентности, исчисляемого для трансмонной реализации Willow первыми сотнями микросекунд, успевают проявлять себя и одновременно возникающие двойные, тройные и даже более масштабные (и потому, к счастью, более редкие) ошибки. В этом случае возможностей d-3 уже откровенно не хватает.
В 2018 г., как уже говорилось, квантовая лаборатория Google продемонстрировала уже 72-кубитную версию трансмонного квантового процессора с алгоритмом коррекции d-5: соответственно, рабочие кубиты здесь располагаются массивом 5×5, а оставшиеся 47 (из общего их количества — 72) представляют собой контрольные, точно так же размещённые в условных чёрных полях шахматной доски. Таким образом, удалось добиться уверенного обнаружения и исправления не только одной, но и двух одновременно возникающих в ходе квантовых вычислений ошибок (второй уровень глубины коррекции). Правда, чисто математическая вероятность получить неверный итоговый результат квантовых вычислений (вне зависимости от того, какое число ошибок на конкретных кубитах его спровоцировало) уменьшилась не слишком сильно: если для 17-кубитного чипа она составляла примерно 0,6% для каждого вычислительного цикла, то в случае 72-кубитного этот показатель сократился всего-то до 0,3%. Тем не менее тщательно проведённые эксперименты засвидетельствовали, что снижение это статистически значимое (выходит за пределы ошибок самих измерений) — и, стало быть, есть смысл продолжать наращивать число рабочих кубитов на чипе.
Что, собственно, наконец-то подводит нас к 105-кубитному Willow образца 2024 г., у которого коррекция ошибок производится по схеме d-7: рабочих кубитов здесь 49 (7×7, всё верно), контрольных — 56, а число одновременно фиксируемых и исправляемых ошибок (глубина коррекции) — 3. Частота встречаемости ошибок в итоговых вычислениях для 105-кубитного квантового процессора на трансмонах упала до 0,143% за один вычислительный цикл (сам цикл коррекции ошибок занимает, кстати, 1,1 мкс, а период сохранения когерентности системой в целом — около 100 мкс) — это примерно вдвое меньше, чем в случае 72-кубитного. Более того: за счёт непрерывной коррекции индивидуальных, парных и троичных ошибок общая продолжительность сохранения когерентности логического кубита целиком — т. е. всей 105-кубитной в данном случае системы — выросла примерно вдвое по сравнению с тем же самым временем для одного-единственного физического кубита. И это крайне воодушевило исследователей: понятно, что более крупную структуру сложнее изготовить со строгим выдерживанием всех параметров на каждом участке (что должно обеспечивать идентичность искусственных атомов, — мы уже говорили о важности минимизации числа дефектов в них). Но раз одновременно с увеличением масштаба квантового процессора растёт продолжительность времени его когерентности (как целого) и снижается вероятность возникновения ошибок, — это вселяет самые радужные надежды на ускорение прогресса квантовых вычислений как целого.
Правда, внимательный читатель уже наверняка заметил сделанную чуть выше важную оговорку: все Willow, от первого 17-кубитного прототипа до нынешнего 105-кубитного героя новостей, представляют собой реализацию одного-единственного логического кубита. И рабочие, и контрольные физические его компоненты нацелены лишь на то, чтобы поддерживать когерентность макроскопической квантовой системы как целого. А значит, чтобы взломать, например, 1024-битный код шифрования, потребуется система, в которой взаимосогласованно — то бишь в условиях квантовой запутанности — работают 1024 105-кубитных Willow. Пока же даже два таких процессора расположить рядом, чтобы обеспечить совместную работу хотя бы двух логических кубитов, невозможно, — по крайней мере, подобную задачу исследователи перед собой ещё не ставили. С учетом того, что поверхностный код d-7 позволяет достигать точности 10−3 для 105-кубитной системы, выход на точность 10−6, характерную для ранних ЭВМ середины прошлого века, потребует организации логического кубита по схеме d-27, — то есть из 1457 физических.
Вот, собственно, почему для испытаний свежей версии Willow применялся предельно синтетический (в смысле, не имеющий в принципе никаких реальных приложений) тест на случайную выборку (random circuit sampling), — практических, прикладных задач, в которых однокубитные компьютеры блистали бы на фоне фон-неймановских машин, попросту не существует. По той же причине и 256-битному алгоритму криптографического хеширования, что выполняет ключевую роль в обеспечении целостности данных блокчейна (и лежит в основе биткойна, в частности), на данный момент ничего не угрожает — запустить достаточное количество квантово запутанных логических кубитов для взлома подобного шифра удастся ещё очень-очень нескоро. «Мы создали систему, которая в принципе может масштабироваться — и которую нам теперь придётся масштабировать на практике», — без прикрас сформулировал текущее состояние дел на наиболее передовом участке квантово-вычислительного фронта Кевин Затцингер (Kevin Satzinger), один из ведущих исследователей квантового подразделения Google.
И действительно: если процент ошибок, допускаемых при вычислениях одним логическим кубитом Willow, всего лишь уполовинивается при примерном удвоении числа физических, — это какого же размера должна оказаться квантовая микросхема, готовая обеспечить точность 10−10? И какими выйдут габариты (плюс масса и энергопотребление) охладителя, готового обеспечить перевод столь гигантских пластин в сверхпроводящее состояние? А чтобы решать на подобного рода вычислителях подлинно насущные задачи, придётся ещё и запутывать между собой такие мегакубиты, — это отдельная инженерная задача, к которой пока не очень понятно, как в принципе подступиться. Так что квантовые компьютеры на трансмонах, хотя и бесспорно прогрессируют, делают это крайне неторопливо — на радость всем пользователям защищённых цифровых каналов связи и держателям криптовалют.
Материалы по теме
- Юлихский суперкомпьютерный центр получил 100-кубитный квантовый компьютер Pasqal.
- Nvidia поможет Google в разработке эффективных квантовых процессоров.
- В Китае установили рекорд по времени удержания квантовых состояний.
- В России создан 50-кубитный ионный квантовый компьютер.
- Квантовые компьютеры оказались слишком слабыми для запуска Doom.

