В 2019 г. исследователи из Google провозгласили, что созданный ими прототип квантового компьютера Sycamore на 53 кубитах выполняет за 200 секунд такой объём вычислений, на который один из мощнейших на тот момент суперкомпьютеров, IBM Summit (в составе которого — 9 216 ЦП и 27 648 ГП), затратил бы около 10 тыс. лет. Иными словами, был продемонстрирован прирост скорости квантовых вычислений (по сравнению с теми, что производят передовые машины на базе архитектуры фон Неймана) примерно в 158 миллионов раз.
Звучит настолько вдохновляюще, что возникает один-единственный вопрос: почему за прошедшие с того момента почти три года квантовые вычислители не начали уже вытеснять классические машины — по меньшей мере из списка мощнейших суперкомпьютеров мира?

Ловушка для захвата положительных ионов, которые под воздействием лазерного излучения в глубоком вакууме играю роль кубитов (источник: University of Chicago)
⇡#Где же логика?
Понятно, что новая технология требует немалых инвестиций, но если она гарантирует притом 158-миллионократный прирост вычислительной мощи — какой вменяемый капиталист (не в ругательном, а в чисто экономическом смысле этого термина) позволит удержать себя от вложений в столь перспективную разработку?
Отчего же тогда Конгресс США одобрил недавно выделение 52 млрд долл. на постройку новых полупроводниковых производств на территории страны? Разве в свете столь убедительного прогресса квантовых вычислений это не то же самое, что в 1930-х вкладываться в развитие новых конезаводов и тележных мануфактур — вместо того чтобы строить асфальтовые дороги и заправочные станции для автомобилей с двигателями внутреннего сгорания?

Для охлаждения вычислителя на базе квантового процессора IBM Eagle до температур, близких к абсолютному нулю, требуется настоящий суперхолодильник (источник: IBM)
И ведь прогресс в области квантовых вычислений с тех пор вроде бы не топтался на месте. За прошедшие годы IBM представила квантовый чип Eagle, включающий 127 кубитов, — тем самым впервые в истории число входящих в единый вычислительный блок кубитов превысило сотню. Стартап QuEra Computing, созданный физиками из Гарвардского университета и Массачусетского технологического института, объявил о создании 256-кубитного квантового симулятора. Наконец, сама Google продолжает совершенствовать квантовый вычислитель Sycamore, улучшая механизмы коррекции ошибок и тем самым покоряя новые высоты производительности.

Главный вычислительный узел Sycamore смотрится более чем внушительно (источник: Google)
Тем не менее полупроводниковые компьютеры в обозримой перспективе явно не собираются сдавать свои позиции: пусть очередные достижения на квантовом фронте провозглашаются с завидной регулярностью, но главным вычислительным инструментом продолжают оставаться старые добрые машины, основанные на архитектуре фон Неймана.
Более того, пресловутая задача, с которой в 2019-м столь триумфально справился Sycamore, оказалась не такой уж неподъёмной для классических ЭВМ: Пань Чжан (Pan Zhang) с коллегами из Института теоретической физики при Академии наук КНР недавно показали, что даже не самой мощной майнинговой ферме с полутора десятками графических адаптеров потребительского класса достаточно будет примерно 15 часов для её решения. Любому суперкомпьютеру из мирового списка топ-100 хватило бы на неё и пары десятков секунд.

Так всё-таки, сможет ли квантовый вычислитель (допустим, он слева) в обозримой перспективе обогнать компьютер архитектуры фон Неймана? (источник: La boite verte)
Выходит, специалисты Google выдавали три года назад желаемое за действительное? Не совсем так: группа Пань Чжана подчёркивает, что энергоэффективность квантового компьютера при решении тестовой задачи действительно неизмеримо выше, чем полупроводниковой ЭВМ, да и главная причина неверной оценки производительности традиционных компьютеров в данном конкретном случае кроется в использовании не самого оптимального алгоритма.

Даже внешне 54-кубитный чип Sycamore заметно отличается от привычных полупроводниковых микросхем, работающих в парадигме бинарной логики (источник: Google)
Другое дело, что произведённые Sycamore на протяжении тех самых 200 секунд вычисления не были точными: квантовый компьютер не искал целенаправленно единственно верный ответ, а отсеивал заведомо неверные, и потому оценочная погрешность полученного им результата составляла около 0,2%.
И вот это уже принципиальный момент. Точность последовательных вычислений на классическом компьютере по сути абсолютная. Хотя при реальных расчётах всё равно не удаётся избежать проблем с округлением и иррациональными числами, фактическая точность определяется разрядностью используемых программой переменных — так что погрешность результата даже для бытовых расчётов не превышает десятитысячных долей процента.

Художественная прорисовка (с раздвинутыми для наглядности в стороны жгутами патрубков) размещения квантового процессора в недрах Sycamore (источник: Google)
Квантовые же компьютеры действуют по иному принципу: они не решают задачу последовательно, исполняя шаг за шагом некий алгоритм, а единовременно производят огромное количество вычислений с разными параметрами по одной и той же схеме, так что в итоге среди полученного вороха ответов остаётся лишь выделить более или менее верный.
Именно эта принципиальная особенность квантовых вычислений разом выступает и как их главное преимущество по сравнению с классическими, и как тягчайшая уязвимость — из-за которой, собственно, в дата-центрах по всему миру до сих пор продолжают работать фон неймановские ЭВМ на базе полупроводниковых СБИС. И ещё долго, очень долго такое положение дел не изменится.

Первый в мире коммерческий квантовый компьютер Q System One (2019 г., 20 кубитов) смонтирован в завораживающем дизайнерском корпусе — кубе со стороной 9 футов (почти 2,75 м), где скрывается мощная система охлаждения (источник: IBM)
⇡#Стопроцентно натуральная аналогия
Важно понимать, что квантовые вычисления качественно отличаются от классических. Эволюция от механических машин к вычислителям на радиолампах и от тех — к транзисторным была количественной: суть фон неймановского подхода к организации вычислений при этом не менялась, алгоритмы де-факто оставались прежними. Сама идея создания квантовых компьютеров родилась не из необходимости в очередной раз ускорить исполнение классических алгоритмов — а из потребности адекватно смоделировать реальные физические явления с учётом квантовых эффектов.
Типичная «наглядная» иллюстрация разницы между бинарным битом и кубитом. Всё вроде бы ясно, но совершенно ничего не понятно (источник: Medium)
Известна практически точная дата, когда был предложен термин «квантовый компьютер». В 1981 г. в Массачусетском технологическом институте проходила конференция по физике и вычислениям, на которой сам Ричард Фейнман (Richard Feynman), чьё имя наверняка известно каждому, кто хотя бы поверхностно интересовался квантовой физикой, выступил с докладом «Имитируя физику» (Simulating Physics). Учёный сформулировал и обосновал важнейший принцип, на котором должна основываться вычислительная система, предназначенная для моделирования реальных квантовых явлений: полное подобие природе (“The computer will do exactly the same as nature”).
Иными словами, для численного моделирования квантовых явлений необходима система, построенная на квантовых же принципах. Как добросовестный исследователь, Фейнман сослался в своём докладе не только на фундаментальную теорему Дж. С. Белла (первая публикация — 1964 г.) о невоспроизводимости квантово-механических феноменов с применением классических вычислительных средств, но и на две более поздние работы на эту тему из-за «железного занавеса» — «Термодинамические модели обработки информации» Р. П. Поплавского (1975 г.) и «Вычислимое и невычислимое» Ю. И. Манина (1980 г.), где указывалось на принципиальную невозможность имитации поведения квантовых систем на традиционных ЭВМ по причине чрезвычайной сложности алгоритмизации квантовых явлений (принципа суперпозиции, прежде всего).

Ричард Фейнман объясняет квантовую физику на пальцах, 1967 г. (источник: Los Angeles Times)
В конце концов, даже если не касаться квантовой физики, а просто моделировать поведение больших ансамблей вполне классических частиц, ограничения архитектуры фон Неймана дают о себе знать более чем недвусмысленно. Скажем, если R частиц могут занимать N положений в пространстве, то полный спектр состояний такой системы определяется как NR (N в степени R) — так что даже для самых современных суперкомпьютеров адекватная эмуляция процессов в такой системе при R и N порядка всего-то 100 уже представляет собой по сути непосильную задачу.
Важнейшая особенность квантового процесса, его кардинальное отличие от привычных нам по окружающему макромиру явлений, — принцип суперпозиции (точнее, принцип существования суперпозиции состояний). Принцип этот подразумевает возможность нахождения квантовой системы в полном спектре доступных ей взаимоисключающих состояний одновременно — до тех пор, пока не будет произведено измерение её состояния наблюдателем, что приведёт к схлопыванию (коллапсу) квантовой системы в некое однозначное. Тот самый кот Шрёдингера, да.

«Мистер Шрёдингер? Сэр? Вы… уверены?» (источник: Pixabay)
Очень часто в популярном изложении суперпозицию «ради лучшего усвоения неподготовленной аудиторией» подменяют стохастикой, случайностью. Скажем, как наглядно пояснить, что некий квантовый объект, способный после измерения представать в дискретных конечных состояниях 0 или 1, вплоть до самого момента этого измерения находится не просто в одном из этих состояний, а также и в любой их суперпозиции — т. е. линейной комбинации с некими коэффициентами, — причём одновременно?
Обычно для иллюстрации здесь используют аналогию с монетой. Подброшенная в воздух, она быстро крутится, и потому определить, орлом или решкой вверх она в итоге выпадет, невозможно: вот, мол, это состояние вращения и есть аналог квантовой суперпозиции. В момент же измерения — когда монета упала на ладонь экспериментатора — происходит фиксация одного из дискретных граничных состояний, «орёл» или «решка».
Слабость этой аналогии в том, что хотя монета действительно вращается в воздухе сложным образом, особенно если её хитро закрутить при подбрасывании, в каждый момент времени её проекция на горизонтальную плоскость — при взгляде сверху — всё-таки практически однозначно демонстрирует либо орла, либо решку. За исключением тех редких мгновений, конечно же, когда она встаёт точно на ребро.

Подбрось монетку — получишь право утверждать, что понимаешь закономерности квантового мира (источник: Unsplash)
Для адекватного представления квантовой суперпозиции, как подчёркивали Фейнман и его предшественники, придётся смириться с тем, что прямых аналогов квантово-механическим системам в привычном для нас макромире не существует. Бессмысленно пытаться постигать суть явления, зависящего не только от каких-то объективных внутренних факторов, но и от того, наблюдает за ним кто-нибудь в данный момент или же нет. И тем, кто всерьёз намерен разобраться хотя бы в азах принципов построения и работы квантовых компьютеров, придётся освоить специфический для этого направления инструментарий — пусть даже на самом базовом уровне.
⇡#Комплексный — не обязательно сложный
Бит — с точки зрения классической вычислительной математики — это система, способная пребывать лишь в одном из двух возможных дискретных состояний: «0» или «1». Однако по опыту повседневности мы интуитивно понимаем, что ничего непрерывного в природе не существует: даже механический тумблер не переходит из верхнего положения в нижнее бесконечно быстро — переключение занимает некое определённое время.
Квантовая физика — это просто, изящно, а главное — математически безупречно строго (источник: Thought Co.)
То же верно для полупроводниковых схем: если полевой транзистор закрыт (не пропускает ток), это может интерпретироваться как «0», открыт (ток идёт) — «1». Однако при подаче управляющего напряжения на затвор ноль обратится в единицу тоже не моментально: сила тока в канале будет нарастать по мере увеличения плотности проходящих по нему электрических зарядов, и лишь какое-то время спустя после открытия затвора (которое само по себе, кстати, тоже не происходит мгновенно) величина тока станет достаточной, чтобы система интерпретировала её как уверенную «1».
В квантовой механике всё принципиально иначе: нет ничего непрерывного — зато есть суперпозиция. Конечные (измеренные наблюдателем) состояния квантовой системы — направление спина электрона, поляризация фотона, энергетические состояния ангармонического осциллятора — при измерении фиксируются мгновенно и однозначно, без переходных периодов и значений. Вместе с тем точно определить состояние квантовой системы можно лишь в момент измерения: до того оно представляет собой ту самую упомянутую выше суперпозицию (или наложение: взвешенную сумму с определёнными особым образом весами) двух взаимоисключающих граничных состояний.

Порой художники, иллюстрируя популярные статьи о квантовых явлениях и объектах, честно стремятся изобразить неизобразимое (источник: Frankfurt Institute for Advanced Studies)
Эти граничные состояния принято обозначать вслед за выдающимся физиком-теоретиком Полем Дираком (Paul Dirac) как |0⟩ и |1⟩ — чтобы сразу было понятно, что речь идёт о квантовой системе с векторами состояний.
Для воспроизведения (моделирования) такой системы при помощи вычислительного средства, которое мы назовём квантовым компьютером, вместо классической реализации битов — которая по очевидным причинам здесь не годится — потребуются квантовые биты, или кубиты (q-bits, qubits). Кубит представляет собой квантовую же систему с граничными состояниями |0⟩ и |1⟩, описываемую — в соответствии с принципом суперпозиции — волновой функцией |ψ⟩:
|ψ⟩ = c0|0⟩ + c1|1⟩. {1}
Какими должны быть коэффициенты c0 и c1? Вряд ли любыми: мы ведь описываем один кубит с предельными значениями |0⟩ и |1⟩, так что за его пределы (как бы само понятие «предела» ни интерпретировать в рамках квантовой механики) волновой функции выходить нелогично.
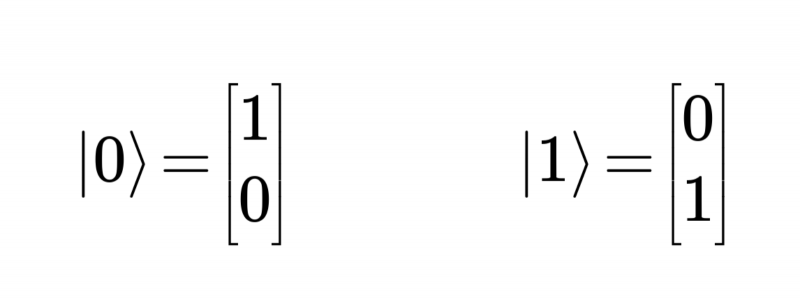
Два базовых вектора состояний кубита, в виде линейной комбинации (взвешенной суммы) которых может быть представлено любое его допустимое состояние
Достаточно очевидно (как раз из того, что в предельных случаях волновая функция будет обращаться либо в |0⟩, либо в |1⟩), что c0 и c1 должны быть нормированы — т. е. должны меняться, причём взаимно согласованно, по модулю величины в пределах от 0 до 1, примерно как катеты вписанного в окружность прямоугольного треугольника, гипотенуза которого совпадает с диаметром:
|c0|2 + |c1|2 = 1. {2}
Здесь проступает довольно ясный физический смысл этих коэффициентов — точнее, квадратов их модулей (заметим, что в формуле {2} вертикальные линии — обозначения модулей чисел, не имеющие отношения к нотации Дирака): это вероятность обнаружить данный кубит в соответствующем граничном состоянии, т. е. либо |0⟩, либо |1⟩.

Тригонометрическая аналогия между квадратами модулей собственных векторов кубита и вероятностью обнаружить его в том или ином состоянии
Но почему речь идёт именно о модулях? Да потому, что коэффициенты c0 и c1 — комплéксные числа. Строго говоря, сам Дирак определял состояние квантовой системы как кет-вектор — луч в сепарабельном гильбертовом пространстве, — но углубляться в тонкости теории множеств в рамках сравнительно популярного материала было бы, право, излишне.
Важно, что тяга к использованию комплексных чисел (при всей их кажущейся противоестественности с точки зрения повседневного опыта обитателей макромира) — вовсе не прихоть физиков-теоретиков, а проявление фундаментальных свойств нашей Вселенной в целом. Дело в том, что, согласно основной теореме алгебры, только в пространстве комплексных чисел любой многочлен степени n (с комплексными же коэффициентами при каждом из членов) имеет ровно n корней.
Это уже более корректное схематическое представление кубита как математической сущности (а не просто как сферы с непонятными точками и линиями), но, чтобы разобраться, что здесь к чему, потребуется приложить определённые усилия (источник: Medium.com)
Поскольку необходимо, чтобы уравнение {1}, типичный многочлен первой степени, имело решение во всех случаях, следует использовать именно комплексные числа — хотя на деле в целом ряде практических приложений коэффициенты c0 и c1 будут-таки оказываться вещественными. Просто потому, что привычные и понятные в макромире вещественные числа — не более чем подмножество комплексных.
⇡#И опять — аналоговые вычисления
Справедливость известной студенческой поговорки «По-настоящему сложной математика становится, когда из неё пропадают цифры» в полной мере ощущают на собственном опыте дерзнувшие разобраться в том, на каких всё-таки основаниях зиждется сама концепция квантовых вычислений. Очень здорово помогает здесь то, что математика — как наука, оперирующая чистыми отвлечёнными сущностями, без привязки к грубому материальному миру — густо пронизана аналогиями, порой парадоксальными, порой невероятно красивыми. Для лучшего понимания кубитов как математических объектов тоже нашлась аналогия — причём снова из тригонометрии, как это ни странно.
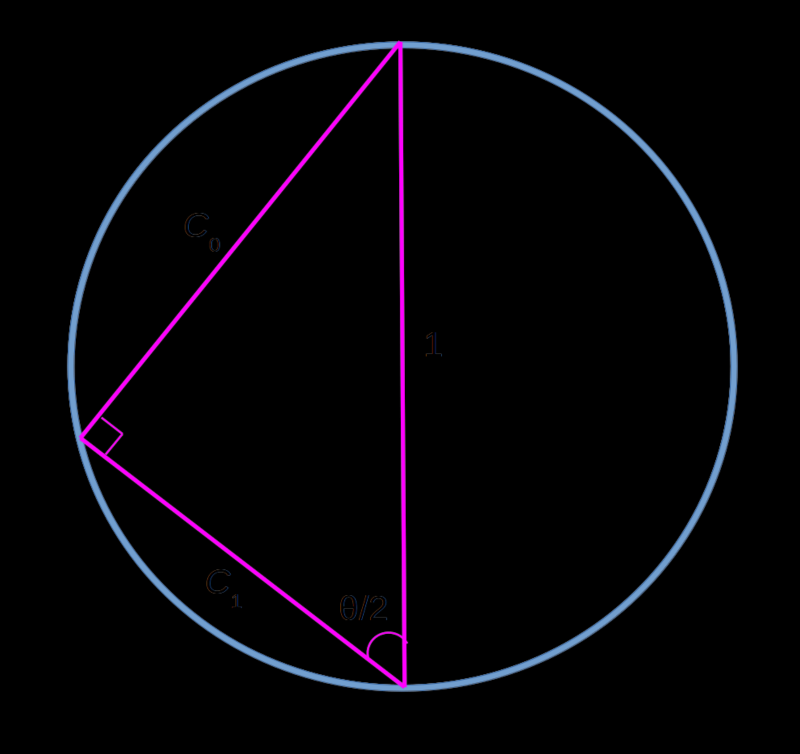
Почти тот же рисунок, что чуть раньше, — но теперь это основное тригонометрическое тождество в приложении к прямоугольному треугольнику с единичной гипотенузой
Итак, прямым аналогом уравнению {2}, в котором, напомним, фигурируют нормированные взаимозависимые коэффициенты, можно считать основное тригонометрическое тождество — безыскусное приложение теоремы Пифагора к прямоугольному треугольнику с единичной гипотенузой:
cos²(θ/2) + sin²(θ/2) = 1. {3}
Обозначение угла можно взять любое; θ/2 здесь принято исключительно ради удобства и красоты последующих выкладок. Теперь снова вспомним, что коэффициенты c0 и c1 (с которыми мы по некой, хотя и обоснованной прихоти сопоставили сейчас косинус и синус некоего угла) — комплексные числа. А те, в свою очередь, можно представить как векторы на комплексной плоскости, где ось абсцисс — вещественная, а ось ординат — мнимая. Тогда комплексному числу P = a + ib, у которого вещественная часть равна a, а мнимая b, будет соответствовать выходящий из начала координат вектор, указывающий в точку (a, b).
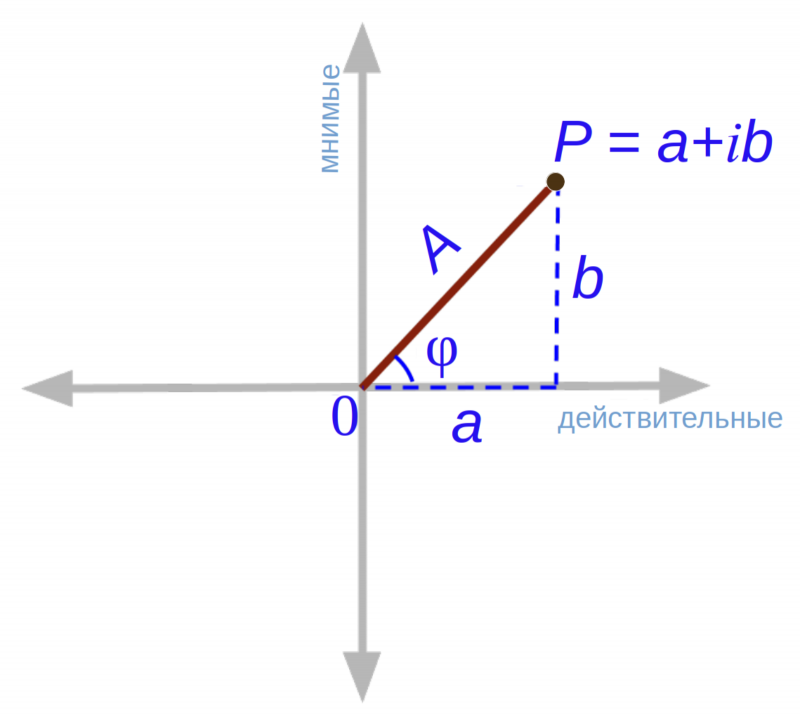
Комплексное число на комплексной же плоскости можно представлять и в прямоугольных координатах, и в полярных — как удобнее
Но этот же самый вектор допустимо представить не в прямоугольных координатах, а в полярных: тогда P = A * eiφ, где A² = a²+ b² (A — модуль величины комплексного числа), а φ — так называемая фаза, тангенс которой равен частному от деления b на a в получившемся прямоугольном треугольнике.
Возвращаемся к волновой функции: действительная и мнимая части комплексного числа у нас есть — это коэффициенты c0 и c1, причём исходя из заданной формулой {3} параметризации очевидно, что пределы изменения угла φ (в нашем случае — θ/2), что бы тот ни обозначал, должны простираться от 0 до π радиан. Если φ превысит π, то один из модулей окажется отрицательным, что противоречит самому математическому смыслу этого понятия (длина вектора может быть в вырожденном случае нулевой, но никак не отрицательной — даже для комплексного числа).

Немного запутались? Ничего страшного: эффект квантовой запутанности, свои ощущения от попытки постичь который изобразил здесь художник, нам вскоре понадобится (источник: Phys.org)
Теперь запишем коэффициенты волновой функции, описывающей наш кубит, с использованием проведённых только что выкладок. Ещё раз отметим, что на данный момент это не более чем игра ума, подставление (правда, осмысленное и внутренне непротиворечивое) одних математических формул в другие:
c0 = cos(θ/2) * exp(iφ0), c1 = sin(θ/2) * exp(iφ1), {4}
то есть уравнение {1} превращается в
|ψ⟩ = cos(θ/2) * exp(iφ0) |0⟩ + sin(θ/2) * exp(iφ1) |1⟩, {5}
а поскольку углы φ0 и φ1 измеряются на одной и той же плоскости,
|ψ⟩ = exp(iφ0) * (cos(θ/2) |0⟩ + sin(θ/2) exp(i(φ0 – φ1)) |1⟩), {6}
или, отбрасывая за неинформативностью φ0 и переходя к учёту действительно значимой разности фаз (φ = φ0 – φ1; это уже не тот φ, что фигурировал на рисунке, поясняющем представление комплексного числа в полярных координатах) вместо каждой из них по отдельности, получаем:
|ψ⟩ = cos(θ/2) |0⟩ + eiφ * sin(θ/2) |1⟩. {7}
Что же получается? Есть некая величина, определяемая скалярным числом (модулем) и двумя углами, один из которых меняется в пределах от 0 до π радиан, а другой, по смыслу представляющий собой разность фаз, волен принимать значения от 0 до 2π.
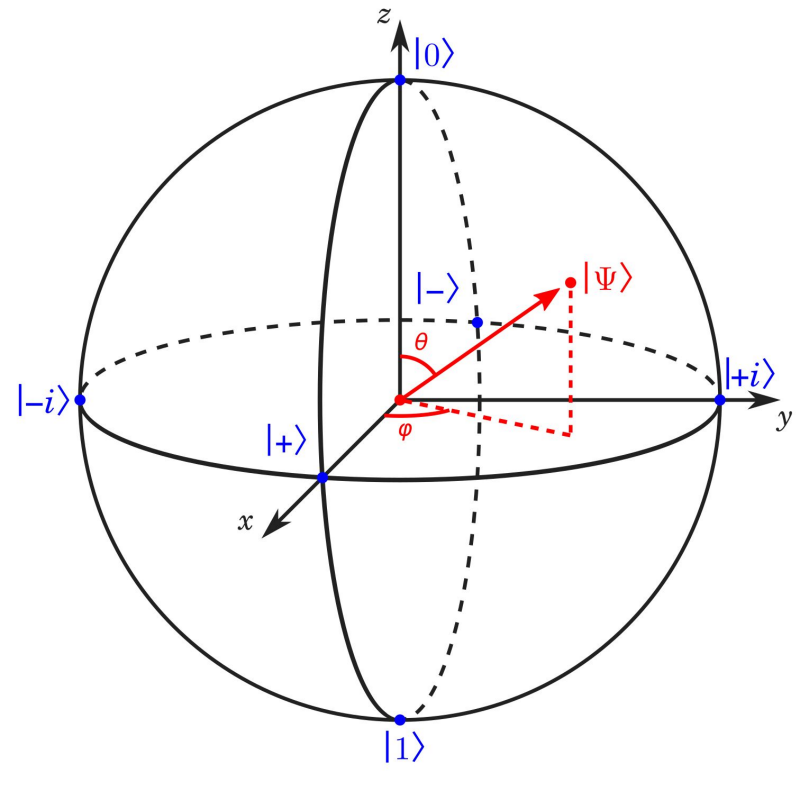
Сфера Блоха окончательно привязывает описание состояний квантовой системы к (сферической) тригонометрии (источник: Prefetch.eu)
Ничего не напоминает? Ну конечно же, это сферические координаты, где θ — азимутальный угол, а φ — полярный. Внезапно выяснилось, что состояние одиночного кубита с ровно двумя граничными состояниями описывается множеством точек на так называемой сфере Блоха (Bloch sphere), причём состояние θ = 0 соответствует значению |ψ⟩ = |0⟩, тогда как при θ = π получаем |ψ⟩ = |1⟩.
⇡#Ваше слово, товарищ Шор
Разобравшись с тем, как можно математически представить волновую функцию кубита, вернёмся к задачам собственно вычислительным. А именно: для чего, собственно, квантовые компьютеры нужны? Какие проблемы, недоступные фон неймановским ЭВМ за разумное время, они позволяют эффективно решать?

Перспективные квантовые компьютеры, даром что имеют дело с единичными атомами, напоминают по обводам и массе фантастические боевые машины (источник: Quantinuum)
Весьма наглядный пример такой задачи предложил в 1994 г. Питер Шор (Peter Shor), математик из Массачусетского технологического института. Он рассмотрел одну из старейших задач вычислительной математики, до сих пор не решённую аналитическими методами — факторизацию числа, — и теоретически показал, как некая не существовавшая на тот момент вычислительная машина, действуя в соответствии с принципами квантовой механики, сможет справиться с этой проблемой за гораздо более разумное время, чем фон неймановская ЭВМ.
Факторизация — это разложение целых положительных (натуральных) чисел на простые множители. Для небольших чисел её тривиально произвести вручную: 6 раскладывается на 2 и 3, 15 — на 3 и 5 и т. д. Но если число достаточно велико, записывается десятками и сотнями значащих цифр, его факторизация превращается в натуральный вычислительный кошмар. Математиками предложен целый ряд алгоритмов, призванных ускорить факторизацию больших чисел на классических компьютерах, но прорывного выигрыша по времени (по сравнению с незатейливым последовательным перебором простых чисел из таблицы — и лобовой проверкой, делится ли изучаемое большое число на них нацело) они всё-таки не дают.
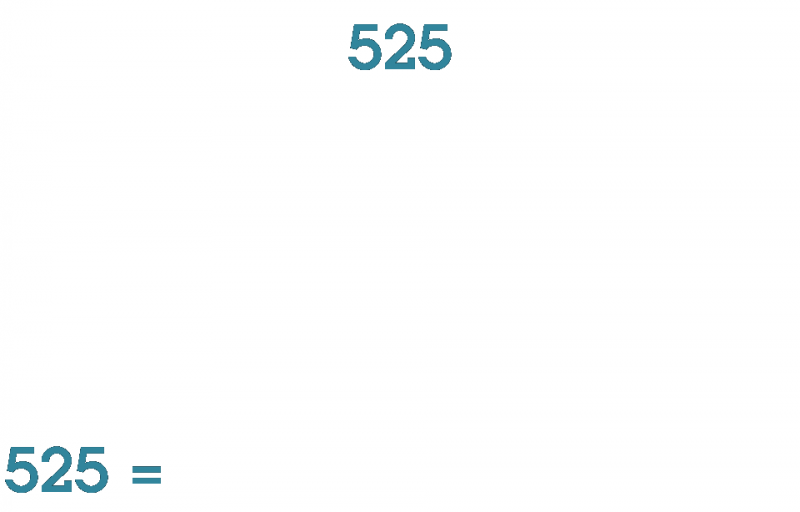
Пошаговая факторизация числа 525: на каждом шаге получается очередной простой множитель (источник: Wikimedia Commons)
Это, кстати говоря, вовсе не плохо — с точки зрения цифровой криптографии. Наоборот: если бы вдруг завтра кто-то обнаружил аналитический способ факторизации больших чисел, под угрозой оказался бы алгоритм шифрования RSA, который применяется сегодня буквально везде — от кодирования данных внутри закрытых от постороннего глаза папок на локальном жёстком диске до передачи чувствительных данных (номеров банковских карт при оплате товаров онлайн, например) через Интернет.
Существенная часть реализации RSA заключается в том, что по открытому каналу получателю зашифрованного сообщения передаётся произведение двух достаточно больших натуральных чисел — представленных сотнями, даже тысячами бит каждое. Факторизовать это произведение — разложить его на исходные множители, даже точно зная, что тех всего два и что оба они простые числа, — для фон неймановской машины чрезвычайно ресурсоёмкая задача. Квантовый же компьютер, действуя по алгоритму Шора, решит эту проблему быстро и эффективно.

8-кубитовый квантовый процессор калифорнийского стартапа Rigetti (2018 г.) для алгоритма RSA угрозы не представляет (источник: Skoltech)
В основе алгоритма Шора лежит сведение разложения на множители к другой задаче, куда лучше оптимизированной для решения на квантовом компьютере, — к поиску периода некой функции. Всё верно: опять налицо тяга различных явлений, описываемых схожими математическими моделями, к взаимному соответствию (аналогии). С привлечением теоремы Эйлера выясняется, что на основе разлагаемого на множители числа нетрудно составить числовой ряд, который — начиная с некоторого момента — гарантированно начнёт повторяться.
Не будем углубляться в математическое изложение этой процедуры — приведём для наглядности лишь один пример из блестящего описания алгоритма Шора, сделанного Скоттом Ааронсоном (Scott Aaronson), профессором Техасского университета в г. Остин. Всем известна последовательность целочисленных степеней двойки:
2, 4, 8, 16, 32, 64, 128, 256…
Каждый из членов этой последовательности может быть взят по модулю любого числа, например 15. Напомним, что «взять x по модулю y» (x mod y) означает «получить остаток от деления x на y нацело». Если делимое меньше делителя, то частное обращается в ноль, а остаток с очевидностью равен самому делимому. Построим новый ряд на основе прежнего:
2 mod 15 = 2,
4 mod 15 = 4,
8 mod 15 = 8,
16 mod 15 = 1,
32 mod 15 = 2,
64 mod 15 = 4,
128 mod 15 = 8,
256 mod 15 = 1
…
Видите закономерность? Вместо ряда бесконечно увеличивающихся чисел (степеней двойки) получился весьма компактный бесконечно повторяющийся ряд с некоторым периодом, в данном случае равным 4 (один за другим повторяются именно четыре числа: 2, 4, 8, 1). Так вот, если в качестве того самого модуля, по которому производится разложение, взять произведение двух простых чисел p и q (а в примере Скотта Ааронсона 15 — это как раз 3 * 5), то период полученной последовательности, как показал Шор, будет нацело делить произведение (p – 1)*(q – 1).
⇡#К вопросу о множественности миров
Наконец-то подходит время собрать воедино всё то, что до сих пор было сказано о квантовых вычислениях, кубитах и принципе суперпозиции, чтобы понять, в чём же всё-таки сила — и одновременно слабость — квантовых вычислений в сравнении с классическими.

Одна из основных слабостей современных реализаций квантовых компьютеров — их невероятная физическая громоздкость (источник: Quantinuum)
Суть метода Шора — в том, что, хотя напрямую из произведения (p – 1)*(q – 1) простые множители p и q получить нельзя, никто не запрещает вычислить периоды множества последовательностей вида
x mod pq,
x2 mod pq,
x3 mod pq,
x4 mod pq...
для множества же случайным образом подобранных x.
Допустим, есть некая машина, квантовый компьютер, которая благодаря принципу суперпозиции способна производить вычисления по алгоритму Шора для одного и того же исследуемого числа (произведения простых p и q), — но для огромного количества случайных аргументов x параллельно. Система же подчиняется законам квантовой механики — значит, способна пребывать во множестве взаимоисключающих состояний одновременно.

Многомировая интерпретация квантовой механики постулирует одновременное существование «параллельных вселенных» с идентичными законами природы и мировыми константами, но находящихся в различных квантовых состояниях (источник: Wikimedia Commons)
Результатами проведённых вычислений будут волны — повторяющиеся последовательности с определёнными периодами. Используя квантовое преобразование Фурье, своего рода проявление интерференции между квантовыми состояниями, не составит труда выделить истинный период — тот самый, что будет нацело делить упомянутое выше произведение (p – 1)*(q – 1).
Здесь в полный рост проявляет себя принципиальное отличие квантовой механики от теории вероятностей, с которой её часто смешивают в популярных изложениях (помните приведённый ближе к началу статьи пример с крутящейся монеткой, якобы поясняющий принцип действия кубита?) В теории вероятностей вероятность любого случайного события строго положительна, тогда как амплитуда волновой функции в общем случае величина комплексная — и вполне может быть отрицательной.

Обычную (не квантовую) интерференцию волн от множественных источников можно наблюдать в дождь в самой обычной луже (источник: Pixabay)
Именно поэтому алгоритм Шора работает за счёт так называемой деструктивной интерференции: амплитуды происходящих параллельно (не одновременно, а именно параллельно, словно бы в параллельных вселенных, как о том говорит одна из интерпретаций квантовой механики) множественных волновых колебаний складываются и усиливаются там, где их периоды максимально близки к истинному, и взаимно гасят друг дружку там, где синфазность колебаний отсутствует из-за большого расхождения их периодов с истинным.
Теперь уже, будем надеяться, понятнее, почему в сообщении Google об успехах 52-кубитного квантового вычислителя Sycamore упоминалась 0,2%-ная погрешность полученного результата. Получить нулевую погрешность в ходе деструктивной интерференции можно лишь при бесконечном числе взаимно складывающихся волн, а поскольку кубитов в том эксперименте было задействовано немногим более полусотни, вместо точного ответа исследователи получили некое среднее число плюс определённый интервал допустимых отклонений.
⇡#Темна вода во кубитех
А вот теперь начинается самое интересное, — практическая часть. Шор в своей работе (созданной, напомним, задолго до появления даже первого прототипа квантового компьютера) имел дело с абстракцией, с идеальным вычислительным средством, свободным от случайных сбоев и технологических ограничений. Но ведь даже полупроводниковые интегральные схемы нуждаются в довольно изощрённых аппаратно-программных инструментах коррекции ошибок буквально на каждом этапе выполнения вычислений и обмена данными. Неужели реальные квантовые компьютеры всегда работают ровно так, как того ожидают их разработчики?

Усовершенствованный (с улучшенной коррекцией ошибок) Sycamore планируют применять для моделирования химических реакций — существенно квантовых по своей природе процессов (источник: Phys.org)
Разумеется, нет, — и проблема коррекции ошибок стоит для них даже острее, чем для классических ЭВМ. Хотя реализовать кубиты можно довольно обширным рядом способов, наиболее распространённый сегодня, реализуемый в том числе инженерами Google и IBM, предусматривает интеграцию резонаторов на основе крохотных сверхпроводящих контуров, интегрированных в полупроводниковые микрочипы, — таким образом получаются сравнительно бюджетные и хорошо управляемые квантовые вычислители. Резонаторы могут находиться в одном из двух граничных энергетических состояний (кодирующих |0⟩ и |1⟩).
Под воздействием микроволнового излучения резонатор можно переводить как в одно из этих состояний, так и в любую их комбинацию (допустим, 42% от |0⟩ и 58% от |1⟩). Но вот незадача: только граничные состояния резонатора устойчивы, и потому из любого промежуточного этот квантовый элемент чрезвычайно быстро, за доли секунды, непременно переходит в ближайшее граничное. Это объективный физический процесс, называемый декогеренцией, разрушает суперпозицию волновых функций. Таким образом, само основание алгоритма Шора — деструктивная интерференция — оказывается невозможным вследствие заведомой потери взаимной согласованности колебаний кубитов даже с истинным периодом. Поэтому все вычисления и фиксацию их результатов на реальном квантовом компьютере необходимо проводить за крайне ограниченное время.

Один из ранних прототипов Sycamore (2014 г.) содержал всего 9 кубитов, выстроенных в ряд протяжённостью немногим более 3 мм (источник: Google)
Хуже того: малый по размерам резонатор подвержен воздействию теплового шума, который с неизбежностью влияет на состояние представленного этим устройством кубита. Представление кубита в виде сферы Блоха наглядно показывает, насколько критичными оказываются последствия зашумления работы этого элементарного компонента квантового компьютера.
Ошибки типа «сбой бита» (bit-flip) приводят к инверсии долей компонентов в составе текущего вектора состояния — вместо 42% от |0⟩ и 58% от |1⟩ получается 58% от |0⟩ и 42% от |1⟩. Ошибки типа «сбой фазы» (phase-flip) едва ли не более опасны с точки зрения алгоритма Шора, поскольку сдвигают фазу вектора состояния сразу на π радиан — и тем самым чрезвычайно сильно вредят процедуре деструктивной интерференции.
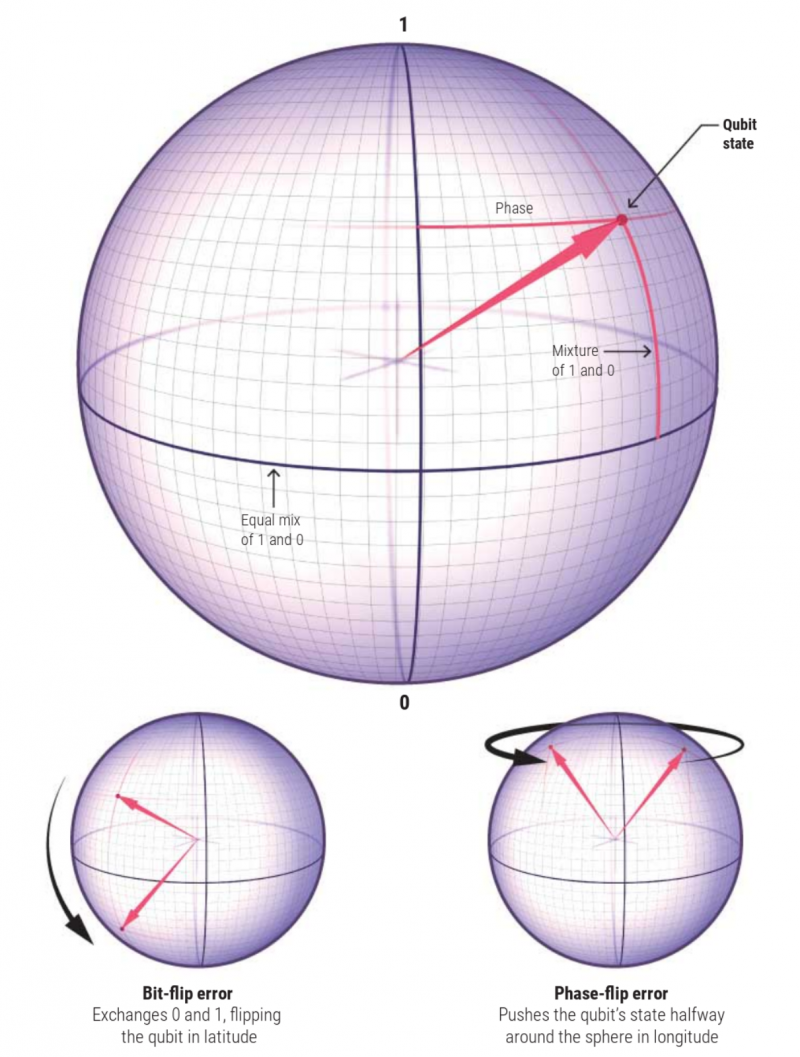
Оба типа ошибок в физических реализациях кубитов снижают точность квантовых вычислений (источник: Science)
По свидетельству Грега Куперберга (Greg Kuperberg), математика из Университета Калифорнии в г. Дэвис, когда команда Google в первый раз запустила на Sycamore свою пресловутую задачу — да-да, ту самую, что на квантовом компьютере исполняется «в 158 миллионов раз быстрее», чем на фон неймановском, — она едва смогла получить корректный ответ как раз из-за шумов, нарушавших деструктивно-интерференционную картину. Фактически примерно 1% информативного сигнала тонул в 99% шума — и только строгая равномерность распределения этого самого шума по измеренным результатам позволила выявить на его фоне даже столь слабые проявления истинного ответа.
Кстати, первым механизм коррекции ошибок предложил всё тот же фон Нейман в 1950-х ещё для компьютеров на радиолампах и механических реле — поскольку те тоже частенько самопроизвольно переходили из нужного состояния в ненужное. Простейшая реализация такого механизма, хотя и довольно накладная, предусматривает утроение каждого логического контура и соответствующее распараллеливание всех проводимых операций.
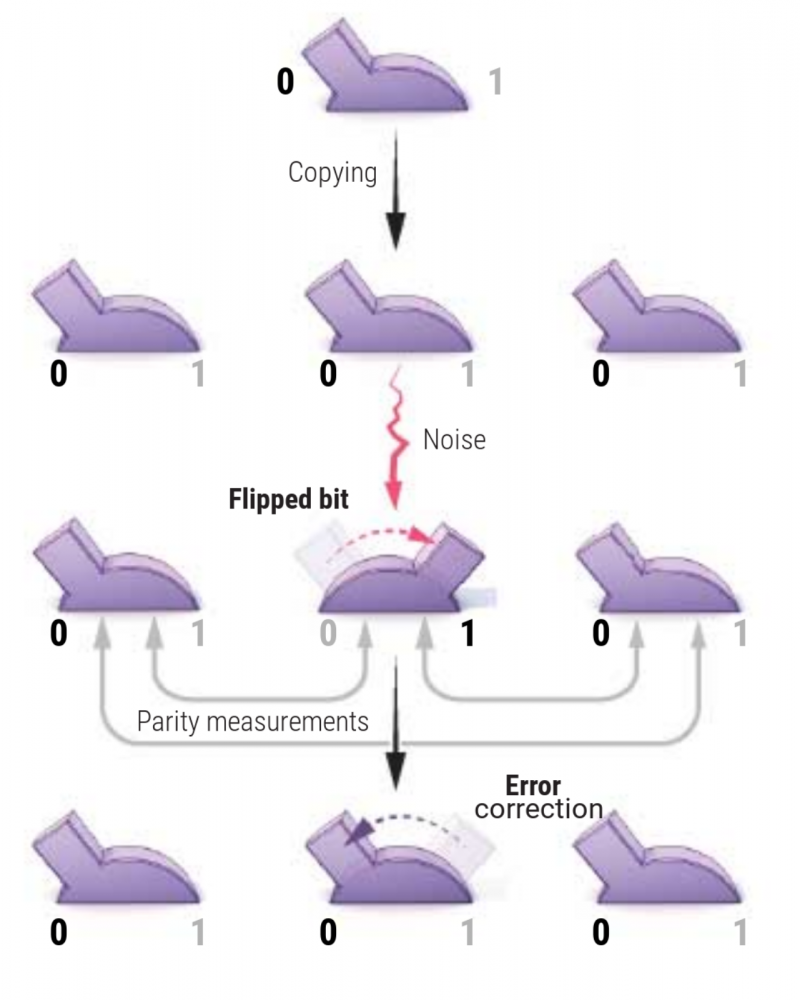
Простой и действенный для фон неймановских машин механизм коррекции ошибок для квантовых вычислений с такой же лёгкостью, увы, реализовать нельзя (источник: Science)
Регулярно сравнивая получаемые на каждом контуре результаты, можно с уверенностью утверждать, что если два из них совпадают, а третий отличается, значит, именно в третьем контуре произошёл какой-то сбой — и тогда на вход следующего участка затроенной логической схемы нужно подать именно то значение, что признано истинным благодаря совпадению первых двух результатов.
⇡#Произошла чудовищная ошибка
Реализовать схему затроения в полупроводниковой СБИС банально просто, хотя это фактически уменьшит втрое число доступных для вычислений транзисторов на чипе, — поэтому в современной микроэлектронике реализуются более изощрённые и менее ресурсоёмкие методы коррекции ошибок. А вот для квантового компьютера реализация даже такой нехитрой схемы представляет собой немалую проблему — опять-таки вследствие объективных тонкостей квантовой механики. Теорема о запрете клонирования прямо указывает на отсутствие способа создать точную копию произвольной квантовой системы (того же кубита), не нарушив притом состояния исходной системы.

Одиночный сверхпроводящий контур, используемый для создания кубита, при большом увеличении (источник: Phys.org)
При этом ничто не мешает двум произвольным квантовым системам находиться в запутанном (взаимозависимом) состоянии, когда, скажем, измерение вектора состояния одного из запутанных кубитов не только выдаёт результат для первого, но и одномоментно переводит второй в точно такое же состояние. Запутывание для квантовых резонаторов на микросхемах реализуется через операцию «контролируемое НЕ» — controlled not (CNOT), аналог «исключающего ИЛИ» (XOR) для бинарной логики. Исходно ведомый кубит переводится в состояние |0⟩, и если ведущий сколлапсировал при измерении в состояние |1⟩, то CNOT меняет состояние ведомого, а в противном случае то остаётся прежним.
Произведя квантовое запутывание трёх кубитов — точнее, двух ведущих с одним и тем же ведомым, — получаем, что если у ведущего вектор состояния образован 42% от |0⟩ и 58% от |1⟩, то и у все трёх вместе вектор состояния будет точно таким же — 42% от |0⟩ и 58% от |1⟩. Подчеркнём, что здесь имеет место не точное копирование первого кубита, физически недопустимое вследствие теоремы о запрете клонирования, а именно создание зависимой (запутанной) структуры из трёх кубитов через логический вентиль. Если после измерения состояния ведущего кубита тот коллапсирует в |1⟩, то и остальные два делают то же самое; если в |0⟩ — значит, все три продемонстрируют состояние |0⟩.
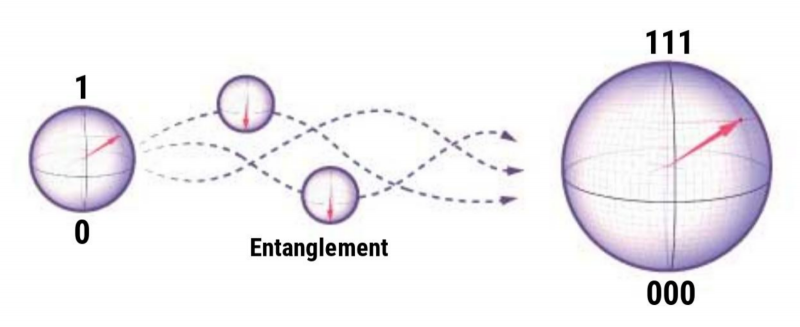
После запутывания состояния ведущего и двух ведомых кубитов оказываются взаимно согласованными (источник: Science)
Далее к этой схеме подключаются ещё два вспомогательных кубита: один — к ведущему и первому ведомому из только что рассмотренной тройки, второй — к первому и второму ведомым. Вспомогательные кубиты позволяют выявлять случаи самопроизвольного изменения конечных состояний каждого из трёх основных кубитов вследствие спонтанно возникающих из-за шума ошибок, не нарушая притом запутанности ведущего с обоими ведомыми. Если первый вспомогательный кубит демонстрирует после измерения значение |0⟩, значит, оба контролируемых им основных кубита находятся в одном и том же состоянии.
Да, в ходе измерения квантовые состояния вспомогательных кубитов коллапсируют, — зато основные продолжают оставаться незатронутыми (неизмеренными). А это значит, что у операторов есть шанс воздействовать микроволновым излучением на перешедший в ошибочное состояние основной кубит до того, как квантовый компьютер решит поставленную перед ним задачу. Тем самым окажется восстановленной когерентность квантовых состояний, необходимая, чтобы деструктивная интерференция в реальной системе сработала хотя бы примерно с той же эффективностью, как в идеальной. Правда, немалой ценой: то, что в теории может делать один кубит, в структуре реального квантового компьютера теперь выполняет взаимоувязанная группа уже из пяти.
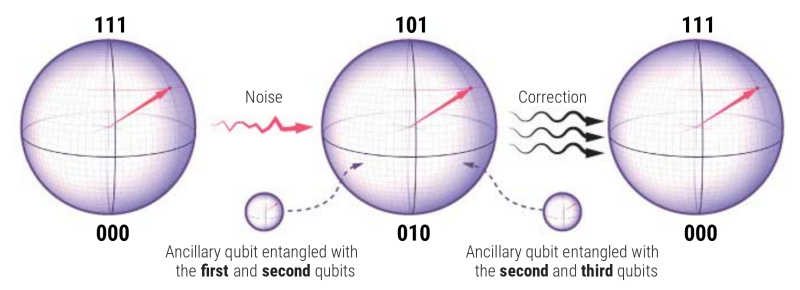
Два вспомогательных (ancillary) кубита, запутанные перекрёстно с тремя основными, позволяют уверенно исправлять одиночные ошибки типа bit-flip (источник: Science)
Увы, этим дело не ограничивается. Описанный механизм коррекции приложим лишь к ошибкам типа «сбой бита»: чтобы выявлять и исправлять ещё и «сбой фазы», требуется схема уже из девяти кубитов, расположенных квадратной матрицей 3 × 3. На этом фоне сообщения о постройке той или иной группой машины с одной или двумя сотнями физических кубитов звучат куда менее бравурно — ведь фактически доступное для вычислений на них число логических (за вычетом вспомогательных) элементов оказывается примерно на 0,5—1 десятичный порядок меньше.
Хуже всего то, что добавление дополнительных элементов в квантовую систему значительно повышает общий уровень шума — и, в свою очередь, порождает необходимость в дополнительной коррекции вновь возникающих ошибок. Допустим, ставится задача факторизовать число, состоящее из 1024 бит, — как раз на такие ключи шифрования сплошь и рядом полагаются далеко не самые изощрённые современные криптографические средства. Решить такую задачу за один проход позволит исполнение алгоритма Шора на квантовом компьютере, состоящем из 1024 логических кубитов.

Предложенная IBM в 2015 г. схема из четырёх кубитов (два основных в запутанном состоянии, два контрольных, занимаемая контуром площадь — 1,6 кв. см) позволяет эффективно выявлять ошибки bit-flip и phase-flip, но не исправлять их (источник: IBM)
При этом — памятуя о существенно ограничивающей время работы системы декогеренции, избежать которой невозможно, — необходимо на крайне ограниченном временнóм отрезке обеспечить точность вычислений на уровне не хуже одной ошибки на миллиард операций. Для чего, по оценке работающей над квантовыми вычислениями в Google физика Мариссы Жюстины (Marissa Giustina), на каждый логический кубит может потребоваться — на нынешнем уровне развития прикладных квантовых технологий — до одной тысячи вспомогательных, реализующих выявление и своевременное (не забываем о растущей со временем угрозе декогеренции!) исправление ошибок. «Говорят, коррекция ошибок — это следующий шаг в квантовых вычислениях. Я бы сказала, что это следующие 25 шагов», — с горькой иронией признаётся исследователь.
⇡#Так есть ли он, реальный прогресс в квантовых вычислениях?
Разумеется, учёные не унывают, — иначе они не были бы учёными. Предлагаются всё более смелые схемы построения квантовых вычислителей — те включают, к примеру, не соседствующие физически на плоскости единого чипа, а разнесённые на заметное расстояние запутанные кубиты. Реализованная в Sycamore и других современных системах схема на квантовых осцилляторах требует расположения кубитов именно по соседству, что делает организацию исправления ошибок на каскадах вспомогательных кубитов чрезвычайно громоздкой. Если использовать другие физические реализации кубитов, позволяющие им взаимодействовать на заметном расстоянии, число вспомогательных элементов в системе удастся радикально сократить за счёт применения оптимальных схем коррекции, — но у таких физических реализаций есть свои, не до конца решённые сегодня проблемы и чисто технические сложности.

127-кубитный квантовый процессор IBM Eagle (2021 г.) полагается для выявления и своевременной коррекции ошибок на новую топологию heavy hex, подразумевающую расположение попарно запутанных основных кубитов в узлах гексагональной решётки, а контрольных — на её гранях (источник: IBM)
Ну и на сладкое: все неурядицы, перечисленные до сих пор, имели отношение к отдельным кубитам, тогда как квантовый компьютер включает, помимо них, и логические элементы — вентили (такие, как упомянутый ранее CNOT). Которые — сюрприз, сюрприз! — тоже подвержены ошибкам. В конце 2021 г. Джон Мартинис (John Martinis), ныне профессор Университета Калифорнии в г. Санта-Барбара, а ранее главный архитектор той самой Sycamore, прямо заявил: «Я думаю, исправление ошибок на квантовых вентилях сегодня куда более важная задача, чем наращивание числа кубитов. В долгосрочной перспективе, если говорить о действительно сложных квантовых вычислениях, следует добиваться снижения уровня ошибок на вентилях до уровня не выше 1%».
Самые передовые квантовые компьютеры наших дней демонстрируют общий уровень логических ошибок (с учётом всех вносящих свой вклад в них узлов и корректирующих схем) порядка 10–3 — грубо говоря, одна-две ошибки на тысячу операций. Чтобы выйти на тот уровень точности, который демонстрируют полупроводниковые вычислители, построенные на архитектуре фон Неймана, требуется точность не менее 10–10, а лучше 10–20. И путь к этому пределу, очевидно, будет долог и труден.

Хотя квантовые вычисления производятся на микроуровне, для обеспечения работы того же 127-кубитного Eagle необходима установка довольно внушительных размеров (источник: IBM)
«Квантовое превосходство», о котором с таким восторгом многие трубили в 2019-м, пока так и не достигнуто — и вряд ли квантовые компьютеры в среднесрочной перспективе станут представлять реальную угрозу RSA и прочим алгоритмам шифрования, полагающимся на факторизацию больших чисел. Однако есть и чему порадоваться: не вызывает сомнений, что в процессе работы над построением подлинно эффективно функционирующего квантового компьютера будет решено такое количество сложнейших технических вопросов и достигнут такой прогресс по направлениям материаловедения, криогеники, микроэлектроники и множества смежных областей, что одно это безусловно оправдает все потраченные на столь долгий тернистый путь силы и средства.
Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.


 MWC 2018
MWC 2018 2018
2018 Computex
Computex
 IFA 2018
IFA 2018













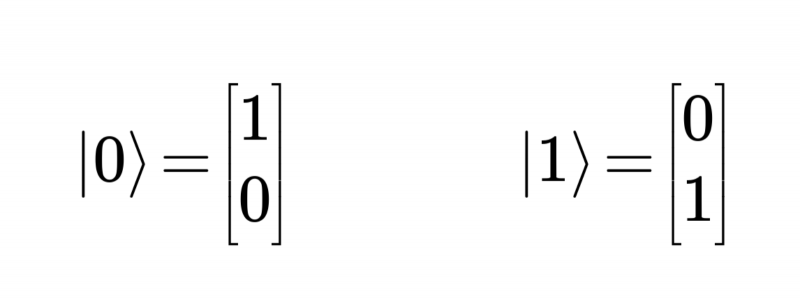







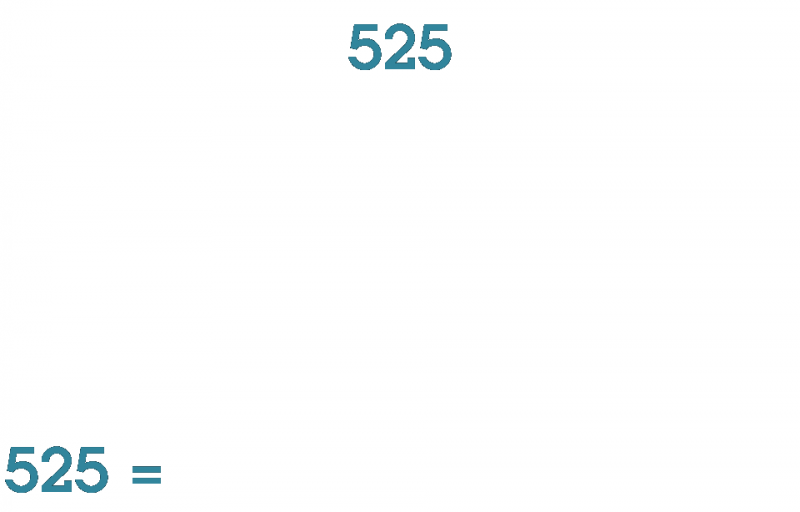




















 Подписаться
Подписаться